How To Draw Angle Bisector Of A Triangle

On the relative lengths of two segments that divide a triangle

In this diagram, BD:DC = AB:AC.

In geometry, the angle bisector theorem is concerned with the relative lengths of the 2 segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

Theorem [edit]

Consider a triangle ABC. Let the bending bisector of angle A intersect side BC at a point D between B and C. The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC:

${\displaystyle {\frac {|BD|}{|CD|}}={\frac {|AB|}{|AC|}},}$

and conversely, if a point D on the side BC of triangle ABC divides BC in the same ratio equally the sides AB and AC, and so AD is the angle bisector of angle ∠ A.

The generalized angle bisector theorem states that if D lies on the line BC, and then

${\displaystyle {\frac {|BD|}{|CD|}}={\frac {|AB|\sin \angle DAB}{|AC|\sin \bending DAC}}.}$

This reduces to the previous version if Advertizing is the bisector of ∠ BAC. When D is external to the segment BC, directed line segments and directed angles must be used in the adding.

The bending bisector theorem is commonly used when the angle bisectors and side lengths are known. It can be used in a calculation or in a proof.

An immediate consequence of the theorem is that the angle bisector of the vertex angle of an isosceles triangle volition also bifurcate the opposite side.

Proofs [edit]

Proof 1 [edit]

In the above diagram, use the police of sines on triangles ABD and ACD:

${\displaystyle {\frac {|AB|}{|BD|}}={\frac {\sin \bending ADB}{\sin \angle DAB}}}$

(1)

${\displaystyle {\frac {|AC|}{|CD|}}={\frac {\sin \angle ADC}{\sin \angle DAC}}}$

(2)

Angles ∠ ADB and ∠ ADC form a linear pair, that is, they are adjacent supplementary angles. Since supplementary angles have equal sines,

${\displaystyle {\sin \angle ADB}={\sin \angle ADC}.}$

Angles ∠ DAB and ∠ DAC are equal. Therefore, the correct paw sides of equations (ane) and (2) are equal, so their left hand sides must also exist equal.

${\displaystyle {\frac {|BD|}{|CD|}}={\frac {|AB|}{|Air-conditioning|}},}$

which is the angle bisector theorem.

If angles ∠ DAB and ∠ DAC are unequal, equations (1) and (ii) can be re-written equally:

${\displaystyle {{\frac {|AB|}{|BD|}}\sin \angle \ DAB=\sin \angle ADB},}$

${\displaystyle {{\frac {|AC|}{|CD|}}\sin \angle \ DAC=\sin \angle ADC}.}$

Angles ∠ ADB and ∠ ADC are nevertheless supplementary, so the right paw sides of these equations are however equal, so we obtain:

${\displaystyle {{\frac {|AB|}{|BD|}}\sin \angle \ DAB={\frac {|Air conditioning|}{|CD|}}\sin \angle \ DAC},}$

which rearranges to the "generalized" version of the theorem.

Proof 2 [edit]

Let D be a signal on the line BC, not equal to B or C and such that Advertizing is not an altitude of triangle ABC.

Permit B ₁ be the base (pes) of the altitude in the triangle ABD through B and permit C ₁ be the base of the altitude in the triangle ACD through C. And then, if D is strictly between B and C, 1 and only one of B _ane or C _i lies inside triangle ABC and it tin exist causeless without loss of generality that B ₁ does. This instance is depicted in the adjacent diagram. If D lies outside of segment BC, then neither B ₁ nor C _ane lies inside the triangle.

∠ DB _ane B and ∠ DC ₁ C are correct angles, while the angles ∠ B _i DB and ∠ C _one DC are congruent if D lies on the segment BC (that is, between B and C) and they are identical in the other cases being considered, then the triangles DB _i B and DC ₁ C are similar (AAA), which implies that:

${\displaystyle {\frac {|BD|}{|CD|}}={\frac {|BB_{1}|}{|CC_{one}|}}={\frac {|AB|\sin \bending BAD}{|AC|\sin \angle CAD}}.}$

If D is the foot of an distance, then,

${\displaystyle {\frac {|BD|}{|AB|}}=\sin \angle \ BAD{\text{ and }}{\frac {|CD|}{|AC|}}=\sin \angle \ DAC,}$

and the generalized form follows.

Proof three [edit]

${\displaystyle \alpha ={\tfrac {\bending BAC}{two}}=\angle BAD=\angle CAD}$

A quick proof tin can be obtained past looking at the ratio of the areas of the 2 triangles ${\displaystyle \triangle BAD}$ and ${\displaystyle \triangle CAD}$ , which are created past the angle bisector in ${\displaystyle A}$ . Computing those areas twice using different formulas, that is ${\displaystyle {\tfrac {one}{2}}gh}$ with base ${\displaystyle g}$ and distance ${\displaystyle h}$ and ${\displaystyle {\tfrac {1}{2}}ab\sin(\gamma )}$ with sides ${\displaystyle a}$ , ${\displaystyle b}$ and their enclosed angle ${\displaystyle \gamma }$ , will yield the desired result.

Let ${\displaystyle h}$ denote the peak of the triangles on base ${\displaystyle BC}$ and ${\displaystyle \alpha }$ be one-half of the angle in ${\displaystyle A}$ . So

${\displaystyle {\frac {|\triangle ABD|}{|\triangle ACD|}}={\frac {{\frac {one}{2}}|BD|h}{{\frac {i}{2}}|CD|h}}={\frac {|BD|}{|CD|}}}$

and

${\displaystyle {\frac {|\triangle ABD|}{|\triangle ACD|}}={\frac {{\frac {1}{2}}|AB||Advertizement|\sin(\alpha )}{{\frac {1}{two}}|Air-conditioning||AD|\sin(\alpha )}}={\frac {|AB|}{|AC|}}}$

yields

${\displaystyle {\frac {|BD|}{|CD|}}={\frac {|AB|}{|Air-conditioning|}}.}$

Exterior bending bisectors [edit]

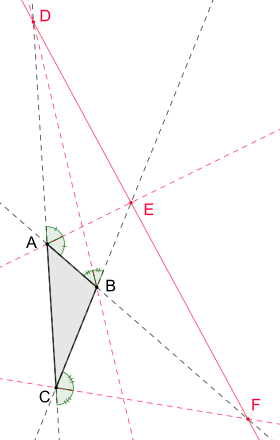
outside bending bisectors (dotted red):
Points D, Eastward, F are collinear and the following equations for ratios hold:
${\displaystyle {\tfrac {|EB|}{|EC|}}={\tfrac {|AB|}{|Air conditioning|}}}$ , ${\displaystyle {\tfrac {|FB|}{|FA|}}={\tfrac {|CB|}{|CA|}}}$ , ${\displaystyle {\tfrac {|DA|}{|DC|}}={\tfrac {|BA|}{|BC|}}}$

For the exterior angle bisectors in a non-equilateral triangle there exist similar equations for the ratios of the lengths of triangle sides. More precisely if the outside angle bisector in ${\displaystyle A}$ intersects the extended side ${\displaystyle BC}$ in ${\displaystyle E}$ , the exterior angle bisector in ${\displaystyle B}$ intersects the extended side ${\displaystyle Air conditioning}$ in ${\displaystyle D}$ and the exterior bending bisector in ${\displaystyle C}$ intersects the extended side ${\displaystyle AB}$ in ${\displaystyle F}$ , then the following equations hold:^[one]

${\displaystyle {\frac {|EB|}{|EC|}}={\frac {|AB|}{|AC|}}}$ , ${\displaystyle {\frac {|FB|}{|FA|}}={\frac {|CB|}{|CA|}}}$ , ${\displaystyle {\frac {|DA|}{|DC|}}={\frac {|BA|}{|BC|}}}$

The iii points of intersection between the exterior angle bisectors and the extended triangle sides ${\displaystyle D}$ , ${\displaystyle East}$ and ${\displaystyle F}$ are collinear, that is they prevarication on a common line.^[ii]

History [edit]

The angle bisector theorem appears as Suggestion 3 of Volume Vi in Euclid'due south Elements. According to Heath (1956, p. 197 (vol. ii)), the corresponding statement for an external bending bisector was given by Robert Simson who noted that Pappus assumed this outcome without proof. Heath goes on to say that Augustus De Morgan proposed that the two statements should be combined as follows:^[3]

If an angle of a triangle is bisected internally or externally by a straight line which cuts the opposite side or the opposite side produced, the segments of that side will take the same ratio as the other sides of the triangle; and, if a side of a triangle be divided internally or externally so that its segments have the aforementioned ratio equally the other sides of the triangle, the straight line drawn from the point of section to the angular point which is reverse to the first mentioned side will bisect the interior or exterior angle at that athwart point.

Applications [edit]

This section needs expansion with: more theorems/results. You lot can assist by adding to it. (September 2022)

This theorem has been used to evidence the following theorems/results:

• Coordinates of the incenter of a triangle

References [edit]

1. ^ Alfred Southward. Posamentier: Advanced Euclidean Geometry: Excursions for Students and Teachers. Springer, 2002, ISBN 9781930190856, pp. 3-iv
2. ^ Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, p. 149 (original publication 1929 with Houghton Mifflin Company (Boston) as Modern Geometry).
3. ^ Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (second ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications.

   (3 vols.): ISBN 0-486-60088-2 (vol. one), ISBN 0-486-60089-0 (vol. two), ISBN 0-486-60090-4 (vol. 3). Heath's authoritative translation plus extensive historical research and detailed commentary throughout the text.

Farther reading [edit]

• M.West.I.Due south Amarasinghe: On the Standard Lengths of Angle Bisectors and the Bending Bisector Theorem, Global Journal of Advanced Research on Classical and Modern Geometries, Vol 01(01), pp. 15 – 27, 2022

External links [edit]

• A Property of Bending Bisectors at cut-the-knot
• Intro to angle bisector theorem at Khan Academy

Source: https://en.wikipedia.org/wiki/Angle_bisector_theorem

Posted by: guntergeopenceed.blogspot.com

Share this post